Dependent censoring and its effect on standard models

What is dependent censoring ?

This post will focus on dependent censoring and its consequences on standard survival models. It is known that the standard models, e.g., the Kaplan Meier estimator for survival function and the Cox proportional hazards model, assume that the survival time (T) is independent of the censoring time (C). This is a crucial assumption for producing valid inferences. Unfortunately, there is no formal test for the independent censoring assumption since we never observe survival time and censoring time simultaneously. Given the difficulty of checking this assumption, the data analysts have often analyzed survival data without warning that their results are valid under the independence assumption. So, this post aims to create awareness among statisticians by showing what will happen when the standard models do not satisfy the independence assumption.

Before moving on to what happens when independent censoring is not satisfied, let me discuss under what scenarios this assumption makes sense. The independence assumption is commonly assumed to obtain identifiability and to allow model estimation without experiencing many difficulties. For instance, the independence assumption makes sense for the administrative censoring mechanism in which the censoring happens at the end of the study. In general, if the mechanism that induces censoring is entirely unrelated to the event of interest, we can do our data analysis under this assumption. However, there are many practical applications where the independent censoring assumption is unrealistic. For example, in medical studies, patients may withdraw from the study because their condition is deteriorating or because they show side effects that need alternative treatments. Here, the reason for withdrawal may be linked to the expected event of interest, which induces dependent censoring.

What happens when independence is assumed but T and C are in reality dependent ?

As I mentioned, the standard models work under the assumption that T is independent of C (given covariates). Let me investigate the effect of deviating from this assumption by giving a numerical example. For example, let $$ T = -\text{log}(u)/\lambda, \quad C = -\text{log}(v)/\lambda, $$ $$ \mbox{where } \lambda = 0.2 \mbox{ and } (u,v) \mbox{ is generated from a Gumbel copula with} $$ $$ \mbox{ parameter } \alpha = 1, 5, \mbox {corresponding to Kendall’s } \tau \mbox{ of 0 and 0.8. } $$ Due to right censoring, we observe $$ Z = \mbox{min} (T,C) \quad \mbox{and} \quad \Delta = I(T \le C). $$ For an arbitrary sample size of n = 300, I calculate the true survival function and the Kaplan-Meier (KM) estimator of the true survival function, which assumes T is independent of C. The data-generating model and simulation steps are summarized in the R chunk below.

library(copula)
library(survival)
set.seed(12346)
n = 300
lambda = 0.2
gumb.cop = gumbelCopula(param = 5, dim =2)  # Gumbel copula
U = rCopula(n,gumb.cop)
T1 = -log(U[,1])/lambda
C = -log(U[,2])/lambda
Z = pmin(T1,C)
delta = as.numeric(T1 <= C)

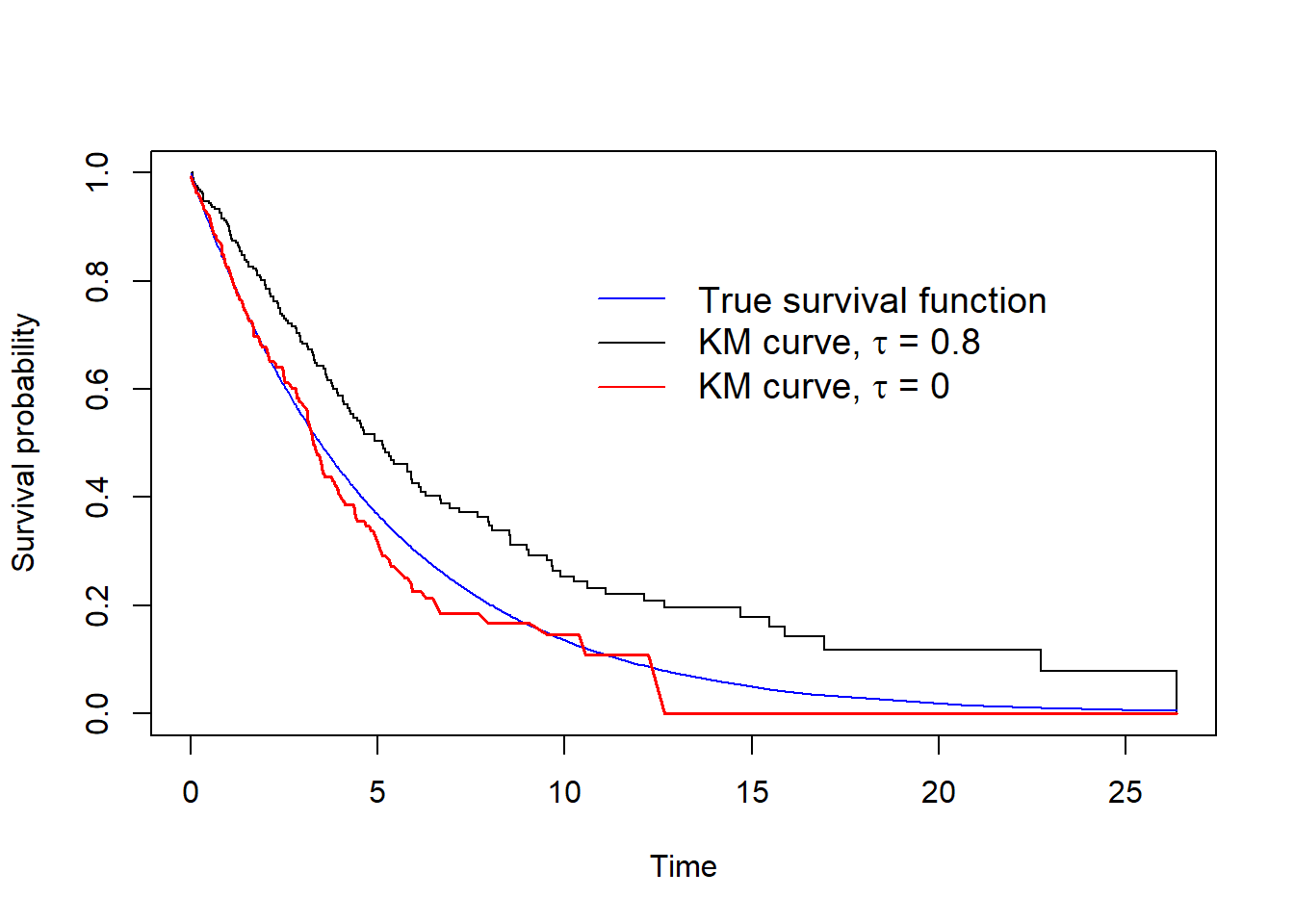
After data generation, the true survival function is estimated using the non-parametric Kaplan-Meier method. The figure below presents the Kaplan-Meier estimator for survival function superimposed on the true survival function for two levels of association.

It can be observed that when 𝝉 = 0 (so there is no dependent censoring), the KM method provides an excellent estimate of the true survival function, as expected. For positive association, 𝝉 = 0.8, we observe that the KM approach overestimates the true survival. The reason is that a positive association between the survival and censoring time indicates that censored individuals will likely have their event soon after their censoring time, whereas under the KM method it is assumed that for a censored observation the (unobserved) survival time can be any value larger than the censoring time, not necessarily a value close to the censoring time.

I hope from this post it is clear that the independence assumption is the most crucial assumption for making correct or unbiased inference based on the standard models.

In next posts, I will cover what can be done when there is a dependent censoring problem. If you want to discuss this topic further, please contact me via the email address on this page.